- Peramalan adalah seni dan ilmu untuk memprediksi masa depan.
- Peramalan adalah tahap awal, dan hasil ramalan merupakan basis bagi seluruh tahapan pada perencanaan produksi.
- Proses peramalan dilakukan pada level agregat (part family); bila data yang dimiliki adalah data item maka perlu dilakukan agregasi terlebih dahulu.
- Metode : Kualitatif dan Kuantitatif.
- Terminologi : perioda, horison, lead time, fitting error, forecast error, data dan hasil ramalan.
Peramalan Eksplanatoris dan Deret Berkala
- Kedua pendekatan ini saling melengkapi dan dimaksudkan untuk jenis penggunaan yang berbeda.
- Pendekatan eksplanatoris mengasumsikan adanya hubungan sebab akibat di antara input dengan output dari suatu sistem.
Persyaratan penggunaan metode kuantitatif :
- Tersedia informasi tentang masa lalu.
- Informasi tersebut dapat dikuantitatifkan dalam bentuk data numerik.
- Dapat diasumsikan bahwa beberapa aspek pola masa lalu akan terus berlanjut di masa mendatang.
Langkah-langkah Peramalan
- Definisikan tujuan peramalan.
- Plot data (part family) masa lalu.
- Pilih metode-metode yang paling memenuhi tujuan peramalan dan sesuai dengan plot data.
- Hitung parameter fungsi peramalan untuk masing-masing metode.
- Hitung fitting error untuk semua metode yang dicoba.
- Pilih metode yang terbaik, yaitu metode yang memberikan error paling kecil.
- Ramalkan permintaan untuk periode mendatang.
- Lakukan verifikasi peramalan.
Pola data metode deret berkala (1)
- Pola Horisontal (H) terjadi bilamana data berfluktuasi di sekitar nilai rata-rata yang konstan.Suatu produk yang penjualannya tidak meningkat atau menurun selama waktu tertentu termasuk jenis ini. Pola khas dari data horizontal atau stasioner seperti ini dapat dilihat dalam gambar 1.1.
- Pola Musiman (S) terjadi bilamana suatu deret dipengaruhi oleh faktor musiman (misalnya kuartal tahun tertentu, bulanan, atau hari-hari pada minggu tertentu). Penjualan dari produk seperti minuman ringan,es krim, dan bahan bakar pemanas ruang semuanya menunjukkan jenis pola ini.
Pola data metode deret berkala (2)
- Pola siklis (C) terjadi bilamana datanya dipengaruhi oleh fluktuasi ekonomi jangka panjang seperti yang berhubungan dengan siklus bisnis. Contoh : Penjualan produk seperti mobil, baja, dan peralatan utama lainnya.
- Pola trend (T) terjadi bilamana terdapat kenaikan atau penurunan sekuler panjang dalam data. Contoh : Penjualan banyak perusahaan, GNP dan berbagai indikator bisnis atau ekonomi lainnya.
Karakteristik Trend
Komponen
|
Amplitudo
|
Penyebab
|
Seasonal
|
12 bulan
|
Liburan, musim, perioda finansial
|
Cyclical
|
3-5 tahun
|
Ekonomi nasional, perubahan politik
|
Bisnis
|
1-5 tahun
|
Pemasaran, kompetisi, performance
|
Product life cycle
|
1-5 tahun, makin pendek
|
Substitusi produk
|
Metode Deret Waktu
- Constant
- Linier Trend
- Quadratic
- Exponential
- Moving Average
- Exponential Smoothing
- Seasonal
1. Metode Constant
- Dalam metode Constant, peramalan dilakukan dengan mengambil rata-rata data masa lalu (historis).
- Rumus untuk constant :
- Keterangan : d’t = Forecast untuk saat tt = time (independent variable)dt = demand pada saat tn = jumlah data
2. Metode Linier Trend
- Model ini menggunakan data yang secara random berfluktuasi membentuk garis lurus.
- Rumus untuk metoda linier :
- Keterangan: d’t = Forecast untuk saat t
- a = interceptb = kemiringan garist = time (independent variable)dt = demand pada saat tn = jumlah data
3. - Metode Quadratic (1)
- Model ini menggunakan data yang secara random berfluktuasi membentukkurva quadratic.
- Rumus untuk model quadratic:
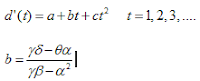Keterangan : ...............
- Metode Quadratic (2)
4. - Metode Exponential (1)
- Digunakan apabila persamaan a dan b tidak bisa dipecahkan dengan carakonvensional.
- Digunakan transformasi logaritma ke dalam situasi regresi.
- Persamaan metode eksponensial :
Keterangan:d’t = Forecast untuk saat ta = interceptb = kemiringan garist = time (independent variable)e = exponential (konstanta)
- Metode Exponential (2)
Persamaan transformasi logaritma :
Keterangan:
d’t = Forecast untuk saat t
a = intercept
b = kemiringan garis
t = time (independent variable)
e = exponential (konstanta)
5. Metode Moving Average (1)
- Digunakan bila data-datanya :
- tidak memiliki trend
- tidak dipengaruhi faktor musim
- Digunakan untuk peramalan dengan perioda waktu spesifik.
- Moving Average didefinisikan sebagai :
- tidak memiliki trend
- tidak dipengaruhi faktor musim
- Metode Moving Average (2)
- Peramalan jangka pendek lebih baik dibandingkan jangka panjang.
- Kelemahan : tidak cocok untuk pola data trend atau pola data musiman.
6. Metode Exponential Smoothing (1)
- Kesalahan peramalan masa lalu digunakan untuk koreksi peramalan berikutnya.
- Dihitung berdasarkan hasil peramalan + kesalahan peramalan sebelumnya.
- Metode Exponential Smoothing (2)
ES didefinisikan sebagai :
Keterangan:
Ft+1 = Ramalan untuk periode berikutnya
Dt = Demand aktual pada periode t
Ft = Peramalan yg ditentukan sebelumnya untuk periode t
a = Faktor bobot
a besar, smoothing yg dilakukan kecil
a kecil, smoothing yg dilakukan semakin besar
a optimum akan meminimumkan MSE, MAPE
7. Metode Seasonal
Demand meningkat karena pengaruh tertentu atau berdasarkan waktu.
Nilai/harga faktor seasonal antar 0 dan 1.
Formulasi peramalan pada tahun ke i :
d’i = a + bt
Keterangan :
d’i = peramalan untuk saat ke i
t = perioda waktu (bulan, minggu, dll)
Formulasi Peramalan Seasonal :
SF(i) = (Si).(d’t)
Forecasting Errors & Tracking Signals
3 metode perhitungan kesalahan peramalan :
Verifikasi (1)
Salah satu metode verifikasi adalah Moving Range Chart (MRC).
Moving Range (MR) didefinisikan sebagai :
MR = |(d’t – dt) – (d’t-1– dt-1 )|
Keterangan :
d’t = ramalan pada bulan ke t
dt = kebutuhan pada bulan ke t
d’t–1 = ramalan pada bulan ke t-1
dt–1 = kebutuhan pada bulan ke t-1
Verifikasi (2)
Rata-rata MR dihitung :
Batas kontrol atas (UCL), batas kontrol bawah (LCL), dan garis tengah (CL)
Verifikasi (3)
Verifikasi (4)
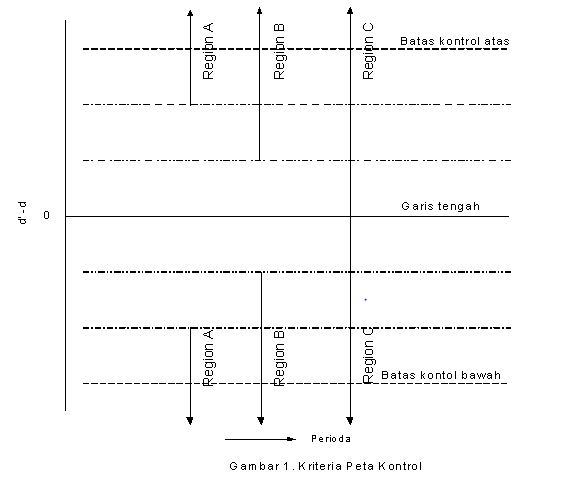
Pengujian out of kontrol :
Dari 3 titik yang berurutan, 2 titik atau lebih berada di daerah A.
Dari 5 titik yang berurutan, 3 titik atau lebih berada di daerah B.
Dari 8 titik yang berurutan, seluruhnya berada di atas atau di bawah center line.
Satu titik berada di luar batas kontrol.
Verifikasi (5)
Contoh Soal : Kasus Peramalan Konstan
Verifikasi (6)
Verifikasi (7)
Bila kondisi out of control terjadi:
Perbaiki ramalan dengan memasukkan data baru.
Tunggu evidence (fakta-fakta) selanjutnya.
Contoh Metode Constant
Bulan t dt
Jan 1 90
Feb 2 111
Mar 3 99
Apr 4 89
Mei 5 87
Jun 6 84
Jul 7 104
Aus 8 102
Sep 9 95
Okt 10 114
Nov 11 103
Des 12 113
∑ = 1191
Contoh Metode Linear Trend
1 2050 2050 1 2108,5 3.422,2
2 2235 4470 4 2210,1 620,0
3 2420 7260 9 2311,7 11.728.9
4 2360 9440 16 2413,3 2.840,9
5 2490 12450 25 2514,9 620,0
6 2620 15720 36 2616,5 12,3
21 14175 51390 91 19.244,3
d’t = a + bt
= 2006,9 + 101,6t
Contoh Metode Quadratic
t
|
t2
|
t3
|
t4
|
dt
|
tdt
|
t2dt
|
1
|
1
|
1
|
1
|
16
|
16
|
16
|
2
|
4
|
8
|
16
|
24
|
48
|
96
|
3
|
9
|
27
|
81
|
34
|
102
|
306
|
4
|
16
|
64
|
256
|
46
|
184
|
736
|
5
|
25
|
125
|
625
|
60
|
300
|
1500
|
∑15
|
55
|
225
|
979
|
180
|
650
|
2654
|
Contoh Metode Eksponensial
t
|
dt
|
Ln(dt)
|
tLn(dt)
|
t2
|
1
|
2.50
|
0.92
|
0.92
|
1
|
2
|
4.12
|
1.42
|
2.84
|
4
|
3
|
6.80
|
1.92
|
5.76
|
9
|
4
|
11.20
|
2.42
|
9.68
|
16
|
5
|
18.47
|
2.92
|
14.60
|
25
|
15
|
9.60
|
33.8
|
55
|
Contoh Metode Moving Average
Bulan t dt MA 3 bulan MA 5 bulan
Jan 1 10 - -
Feb 2 12 - -
Mar 3 13 - -
Apr 4 16 (10+12+13)/3=11,66 -
Mei 5 19 (12+13+16)/3=13,66 -
Jun 6 23 (13+16+19)/3=16,00 (10+12+13+16+19)/5 = 14
Jul 7 26 (16+19+23)/3=19,33 (12+13+16+19+23)/5 = 16,6
Contoh Metode Exponential Smoothing
Period
|
Demand
|
Forecast , Ft+1
| |
a=0.3
|
a=0.5
| ||
1
|
37
|
-
|
-
|
2
|
40
|
37
|
37
|
3
|
41
|
37.9
|
38.5
|
4
|
37
|
38.83
|
39.75
|
5
|
45
|
38.28
|
38.37
|
6
|
50
|
40.29
|
41.68
|
7
|
43
|
43.20
|
45.84
|
8
|
47
|
43.14
|
44.42
|
9
|
56
|
44.30
|
45.71
|
10
|
52
|
47.81
|
50.85
|
11
|
55
|
49.06
|
51.42
|
12
|
54
|
50.84
|
53.21
|
51.79
|
53.61
| ||
Contoh Metode Seasonal (1)
Year
|
Demand (x 1000)
| ||||
Kwartal-1
|
Kwartal-2
|
Kwartal-3
|
Kwartal-4
|
Total
| |
1992
|
12.6
|
8.6
|
6.3
|
17.5
|
45
|
1993
|
14.1
|
10.3
|
7.5
|
18.2
|
50.1
|
1994
|
15.3
|
10.6
|
8.1
|
19.6
|
53.6
|
42
|
29.5
|
21.9
|
55.3
|
148.7
| |
Perhitungan faktor bobot :
S1= D1/SD = 42/148.7 = 0.28
S2 = 0.20
S3 = 0.15
S4 = 0.37
Contoh Metode Seasonal (2)
a = 40.97 b = 4.3
y = 40.97 + 4.3 t
Untuk tahun 1995 (t =4) diperoleh 58.17
Peramalan utk tiap kwartal:
SF1 = S1.F5 = .28 (58.7) = 16.28
SF2 = 11.63
SF3 = 8.73
SF4 = 21.53
Kesimpulan
1.Peramalan merupakan tahapan awal dalam perencanaan sistem operasi produksi.
2.Model yang paling tepat harus dipilih dalam melakukan peramalan.
3.Model yang dipilih dapat dibandingkan dengan model yang lain dengan menggunakan
kriteria minimum average sum of squared errors.
4.Distribusi forecast errors harus dimonitor, jika terjadi bias maka model yang digunakan
tidak tepat.
Tidak ada komentar:
Posting Komentar