Simulasi Montecarlo
• Simulasi Monte Carlo adalah tipe simulasi probabilistik untuk mencari penyelesaiaan masalah dengan sampling dari proses random
• Dasar simulasi Monte Carlo adalah mengadakan percobaan (eksperimen) pada elemen-elemen probabilistik melalui sampling acak.
• Sehingga simulasi Monte Carlo mengizinkan manajer untuk menentukan beberapa kebijakan yang menyangkut kondisi perusahaan.
Tahapan MonteCarlo
1. Membuat distribusi kemungkinan untuk variabel penting
2. Membangun distribusi kemungkinan kumulatif untuk tiap‐tiap variabel di tahap pertama
3. Menentukan interval angka random untuk tiap variabel
4. Membuat angka random
5. Membuat simulasi dari rangkaian percobaan
Diagram Simulasi Monte-Carlo
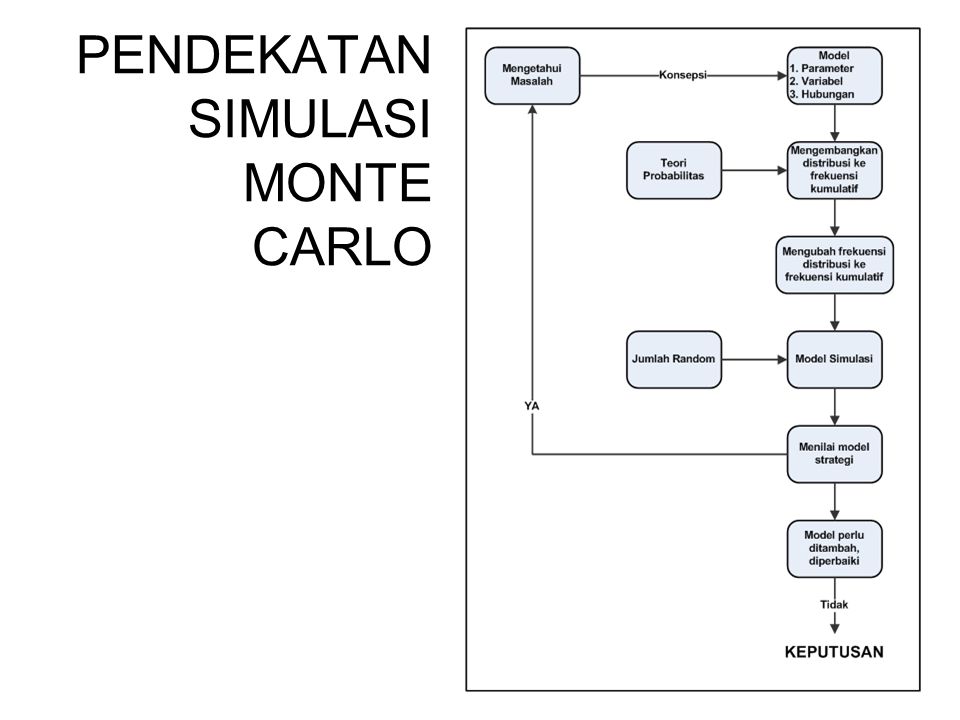
Contoh : (Permintaan Ban)
Setelah melakukan pengamatan selama 200 hari, sebuah toko ban memperkirakan permintaan ban per harinya seperti pada tabel dibawah ini. Toko tersebut hendak memperkirakan permintaan ban untuk 10 hari kedepan.
Permintaan Frekuensi
|
(hari)
|
0
|
10
|
1
|
20
|
2
|
40
|
3
|
60
|
4
|
40
|
5
|
30
|
Total
|
200
|
Penyelesaian :
Langkah 1: Menetapkan distribusi probabilitas
• Tabel Probabilitas Permintaan Ban Radial
Variabel Permintaan
|
Probabilitas
|
0
|
10/200 = 0,05
|
1
|
20/200 = 0,10
|
2
|
40/200 = 0,20
|
3
|
60/200 = 0,30
|
4
|
40/200 = 0,20
|
5
|
30/200 = 0,15
|
Total
|
200/200 =1,00
|
Langkah 2 : Menetapkan distribusi kumulatif
• Tabel Kumulatif Probabilitas
Variabel Permintaan
|
Probabilitas
|
Kumulatif Probabilitas
|
0
|
10/200 = 0,05
|
0,05
|
1
|
20/200 = 0,10
|
0,15
|
2
|
40/200 = 0,20
|
0,35
|
3
|
60/200 = 0,30
|
0,65
|
4
|
40/200 = 0,20
|
0,85
|
5
|
30/200 = 0,15
|
1,00
|
Diagram Probabilitas kumulatif
Langkah 3 : Interval Bilangan Acak
• Tabel Interval Bilangan Acak
Variabel Permintaan
|
Probabilitas
|
Kumulatif Probabilitas
|
Interval Bilangan Acak
|
0
|
10/200 = 0,05
|
0,05
|
01 – 05
|
1
|
20/200 = 0,10
|
0,15
|
06 – 15
|
2
|
40/200 = 0,20
|
0,35
|
16 – 35
|
3
|
60/200 = 0,30
|
0,65
|
36 – 65
|
4
|
40/200 = 0,20
|
0,85
|
66 – 85
|
5
|
30/200 = 0,15
|
1,00
|
86 - 99
|
Langkah 4 : Pembangkit Bilangan Acak
• Tabel Penarikan Bilangan Acak
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
28
|
50
|
78
|
8
|
16
|
61
|
98
|
51
|
45
|
21
|
Tabel Penarikan Bilangan Acak menggunakan excel
Langkah 5 : Menjalankan Simulasi
• Tabel Simulasi Permintaan
Hari
|
Bilangan Acak
|
Hasil Simulasi
|
1
|
28
|
2
|
2
|
50
|
3
|
3
|
78
|
4
|
4
|
8
|
1
|
5
|
16
|
2
|
6
|
61
|
3
|
7
|
98
|
5
|
8
|
51
|
3
|
9
|
45
|
3
|
10
|
21
|
2
|
Total
|
28
|
Rata rata permintaan per hari :
28/10 = 2,8 ban
Kalau dilakukan 100 kali penarikan bilangan acak akan terlihat jelas permintaan ban sesuai dengan masa lalu yang disimulasikan
Kelas : Simpel E
Anggota Kelompok:
1. Puspa Riri Agustiana 201731302
2. Teuku Rifki Dhulul Fata 201731317
3. Maulida Nabila Akbar 201731268
4. Shelli Mailina 201731202
5. Destri 201731228
Sumber bacaan :
https://slideplayer.info/slide/5066563/Simulasi Montecarlo
• Simulasi Monte Carlo adalah tipe simulasi probabilistik untuk mencari penyelesaiaan masalah dengan sampling dari proses random
• Dasar simulasi Monte Carlo adalah mengadakan percobaan (eksperimen) pada elemen-elemen probabilistik melalui sampling acak.
• Sehingga simulasi Monte Carlo mengizinkan manajer untuk menentukan beberapa kebijakan yang menyangkut kondisi perusahaan.

Kalau dilakukan 100 kali penarikan bilangan acak akan terlihat jelas permintaan ban sesuai dengan masa lalu yang disimulasikan
Kelas : Simpel E
Anggota Kelompok:
1. Puspa Riri Agustiana 201731302
2. Teuku Rifki Dhulul Fata 201731317
3. Maulida Nabila Akbar 201731268
4. Shelli Mailina 201731202
5. Destri 201731228
• Simulasi Monte Carlo adalah tipe simulasi probabilistik untuk mencari penyelesaiaan masalah dengan sampling dari proses random
• Dasar simulasi Monte Carlo adalah mengadakan percobaan (eksperimen) pada elemen-elemen probabilistik melalui sampling acak.
• Sehingga simulasi Monte Carlo mengizinkan manajer untuk menentukan beberapa kebijakan yang menyangkut kondisi perusahaan.
Tahapan MonteCarlo
1. Membuat distribusi kemungkinan untuk variabel penting
2. Membangun distribusi kemungkinan kumulatif untuk tiap‐tiap variabel di tahap pertama
3. Menentukan interval angka random untuk tiap variabel
4. Membuat angka random
5. Membuat simulasi dari rangkaian percobaan
Diagram Simulasi Monte-Carlo

Contoh : (Permintaan Ban)
Setelah melakukan pengamatan selama 200 hari, sebuah toko ban memperkirakan permintaan ban per harinya seperti pada tabel dibawah ini. Toko tersebut hendak memperkirakan permintaan ban untuk 10 hari kedepan.
Permintaan Frekuensi
|
(hari)
|
0
|
10
|
1
|
20
|
2
|
40
|
3
|
60
|
4
|
40
|
5
|
30
|
Total
|
200
|
Penyelesaian :
Langkah 1: Menetapkan distribusi probabilitas
• Tabel Probabilitas Permintaan Ban Radial
Variabel Permintaan
|
Probabilitas
|
0
|
10/200 = 0,05
|
1
|
20/200 = 0,10
|
2
|
40/200 = 0,20
|
3
|
60/200 = 0,30
|
4
|
40/200 = 0,20
|
5
|
30/200 = 0,15
|
Total
|
200/200 =1,00
|
Langkah 2 : Menetapkan distribusi kumulatif
• Tabel Kumulatif Probabilitas
Variabel Permintaan
|
Probabilitas
|
Kumulatif Probabilitas
|
0
|
10/200 = 0,05
|
0,05
|
1
|
20/200 = 0,10
|
0,15
|
2
|
40/200 = 0,20
|
0,35
|
3
|
60/200 = 0,30
|
0,65
|
4
|
40/200 = 0,20
|
0,85
|
5
|
30/200 = 0,15
|
1,00
|
Diagram Probabilitas kumulatif
Langkah 3 : Interval Bilangan Acak
• Tabel Interval Bilangan Acak
Variabel Permintaan
|
Probabilitas
|
Kumulatif Probabilitas
|
Interval Bilangan Acak
|
0
|
10/200 = 0,05
|
0,05
|
01 – 05
|
1
|
20/200 = 0,10
|
0,15
|
06 – 15
|
2
|
40/200 = 0,20
|
0,35
|
16 – 35
|
3
|
60/200 = 0,30
|
0,65
|
36 – 65
|
4
|
40/200 = 0,20
|
0,85
|
66 – 85
|
5
|
30/200 = 0,15
|
1,00
|
86 - 99
|
Langkah 4 : Pembangkit Bilangan Acak
• Tabel Penarikan Bilangan Acak
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
28
|
50
|
78
|
8
|
16
|
61
|
98
|
51
|
45
|
21
|
Tabel Penarikan Bilangan Acak menggunakan excel
Langkah 5 : Menjalankan Simulasi
• Tabel Simulasi Permintaan
Hari
|
Bilangan Acak
|
Hasil Simulasi
|
1
|
28
|
2
|
2
|
50
|
3
|
3
|
78
|
4
|
4
|
8
|
1
|
5
|
16
|
2
|
6
|
61
|
3
|
7
|
98
|
5
|
8
|
51
|
3
|
9
|
45
|
3
|
10
|
21
|
2
|
Total
|
28
|
Rata rata permintaan per hari :
28/10 = 2,8 ban
Kalau dilakukan 100 kali penarikan bilangan acak akan terlihat jelas permintaan ban sesuai dengan masa lalu yang disimulasikan
Kelas : Simpel E
Anggota Kelompok:
1. Puspa Riri Agustiana 201731302
2. Teuku Rifki Dhulul Fata 201731317
3. Maulida Nabila Akbar 201731268
4. Shelli Mailina 201731202
5. Destri 201731228
Sumber bacaan :
https://slideplayer.info/slide/5066563/Simulasi Montecarlo
• Simulasi Monte Carlo adalah tipe simulasi probabilistik untuk mencari penyelesaiaan masalah dengan sampling dari proses random
• Dasar simulasi Monte Carlo adalah mengadakan percobaan (eksperimen) pada elemen-elemen probabilistik melalui sampling acak.
• Sehingga simulasi Monte Carlo mengizinkan manajer untuk menentukan beberapa kebijakan yang menyangkut kondisi perusahaan.

Kalau dilakukan 100 kali penarikan bilangan acak akan terlihat jelas permintaan ban sesuai dengan masa lalu yang disimulasikan
Kelas : Simpel E
Anggota Kelompok:
1. Puspa Riri Agustiana 201731302
2. Teuku Rifki Dhulul Fata 201731317
3. Maulida Nabila Akbar 201731268
4. Shelli Mailina 201731202
5. Destri 201731228
• Simulasi Monte Carlo adalah tipe simulasi probabilistik untuk mencari penyelesaiaan masalah dengan sampling dari proses random
• Dasar simulasi Monte Carlo adalah mengadakan percobaan (eksperimen) pada elemen-elemen probabilistik melalui sampling acak.
• Sehingga simulasi Monte Carlo mengizinkan manajer untuk menentukan beberapa kebijakan yang menyangkut kondisi perusahaan.
Tahapan MonteCarlo
1. Membuat distribusi kemungkinan untuk variabel penting
2. Membangun distribusi kemungkinan kumulatif untuk tiap‐tiap variabel di tahap pertama
3. Menentukan interval angka random untuk tiap variabel
4. Membuat angka random
5. Membuat simulasi dari rangkaian percobaan
Diagram Simulasi Monte-Carlo

Contoh : (Permintaan Ban)
Setelah melakukan pengamatan selama 200 hari, sebuah toko ban memperkirakan permintaan ban per harinya seperti pada tabel dibawah ini. Toko tersebut hendak memperkirakan permintaan ban untuk 10 hari kedepan.
Permintaan Frekuensi
|
(hari)
|
0
|
10
|
1
|
20
|
2
|
40
|
3
|
60
|
4
|
40
|
5
|
30
|
Total
|
200
|
Penyelesaian :
Langkah 1: Menetapkan distribusi probabilitas
• Tabel Probabilitas Permintaan Ban Radial
Variabel Permintaan
|
Probabilitas
|
0
|
10/200 = 0,05
|
1
|
20/200 = 0,10
|
2
|
40/200 = 0,20
|
3
|
60/200 = 0,30
|
4
|
40/200 = 0,20
|
5
|
30/200 = 0,15
|
Total
|
200/200 =1,00
|
Langkah 2 : Menetapkan distribusi kumulatif
• Tabel Kumulatif Probabilitas
Variabel Permintaan
|
Probabilitas
|
Kumulatif Probabilitas
|
0
|
10/200 = 0,05
|
0,05
|
1
|
20/200 = 0,10
|
0,15
|
2
|
40/200 = 0,20
|
0,35
|
3
|
60/200 = 0,30
|
0,65
|
4
|
40/200 = 0,20
|
0,85
|
5
|
30/200 = 0,15
|
1,00
|
Diagram Probabilitas kumulatif
Langkah 3 : Interval Bilangan Acak
• Tabel Interval Bilangan Acak
Variabel Permintaan
|
Probabilitas
|
Kumulatif Probabilitas
|
Interval Bilangan Acak
|
0
|
10/200 = 0,05
|
0,05
|
01 – 05
|
1
|
20/200 = 0,10
|
0,15
|
06 – 15
|
2
|
40/200 = 0,20
|
0,35
|
16 – 35
|
3
|
60/200 = 0,30
|
0,65
|
36 – 65
|
4
|
40/200 = 0,20
|
0,85
|
66 – 85
|
5
|
30/200 = 0,15
|
1,00
|
86 - 99
|
Langkah 4 : Pembangkit Bilangan Acak
• Tabel Penarikan Bilangan Acak
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
28
|
50
|
78
|
8
|
16
|
61
|
98
|
51
|
45
|
21
|
Tabel Penarikan Bilangan Acak menggunakan excel
Langkah 5 : Menjalankan Simulasi
• Tabel Simulasi Permintaan
Hari
|
Bilangan Acak
|
Hasil Simulasi
|
1
|
28
|
2
|
2
|
50
|
3
|
3
|
78
|
4
|
4
|
8
|
1
|
5
|
16
|
2
|
6
|
61
|
3
|
7
|
98
|
5
|
8
|
51
|
3
|
9
|
45
|
3
|
10
|
21
|
2
|
Total
|
28
|
Rata rata permintaan per hari :
28/10 = 2,8 ban
Kalau dilakukan 100 kali penarikan bilangan acak akan terlihat jelas permintaan ban sesuai dengan masa lalu yang disimulasikan
Kelas : Simpel E
Anggota Kelompok:
1. Puspa Riri Agustiana 201731302
2. Teuku Rifki Dhulul Fata 201731317
3. Maulida Nabila Akbar 201731268
4. Shelli Mailina 201731202
5. Destri 201731228
Sumber bacaan :



Tidak ada komentar:
Posting Komentar